Arc length parametrization

The arc length formula

If the curve is given by y = f(x). Then we can write r(x) = (x,f(x)). Thus we get the arc
length formula
$$
\begin{equation}

L=\int_{a}^{b} \sqrt{1+\left(f^{\prime}(x)\right)^{2}} d x

\end{equation}
$$
but if y is not given to be the function of x, then we have another method
$$
\begin{equation}

\int_{a}^{b}|| \vec{r}^{\prime}(t)|| d t=\int_{a}^{b}
\sqrt{\left(x^{\prime}\right)^{2}+\left(y^{\prime}\right)^{2}} d t \quad \text { or } \quad
\int_{a}^{b}|| \vec{r}^{\prime}(t)|| d t=\int_{a}^{b}
\sqrt{\left(x^{\prime}\right)^{2}+\left(y^{\prime}\right)^{2}+\left(z^{\prime}\right)^{2}} d t

\end{equation}
$$
In the previous two methods, we consider integrate the speed function w.r.t time, but we can
also integrate the postion function. Notice that both two integration have the same variable
t (time) since the speed function as the position function is realted to time.

So the s(t) function is the integration of the speed funciton from the time a to b (a and b are
the specific point of time) and this is the important part of the reparametrization because we
let the new parametrization connect the old function and the output or the result is the same
what we would like to derive.

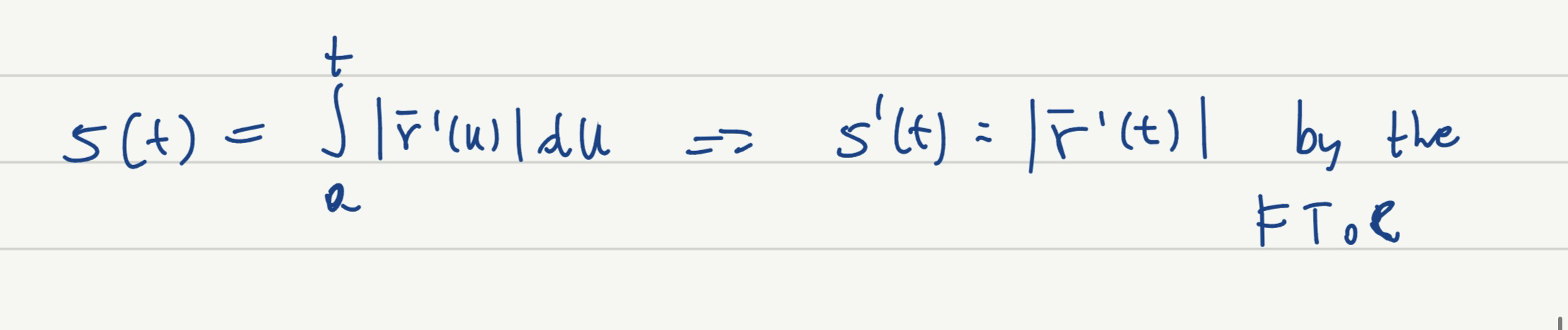
And the pic below is the motivation

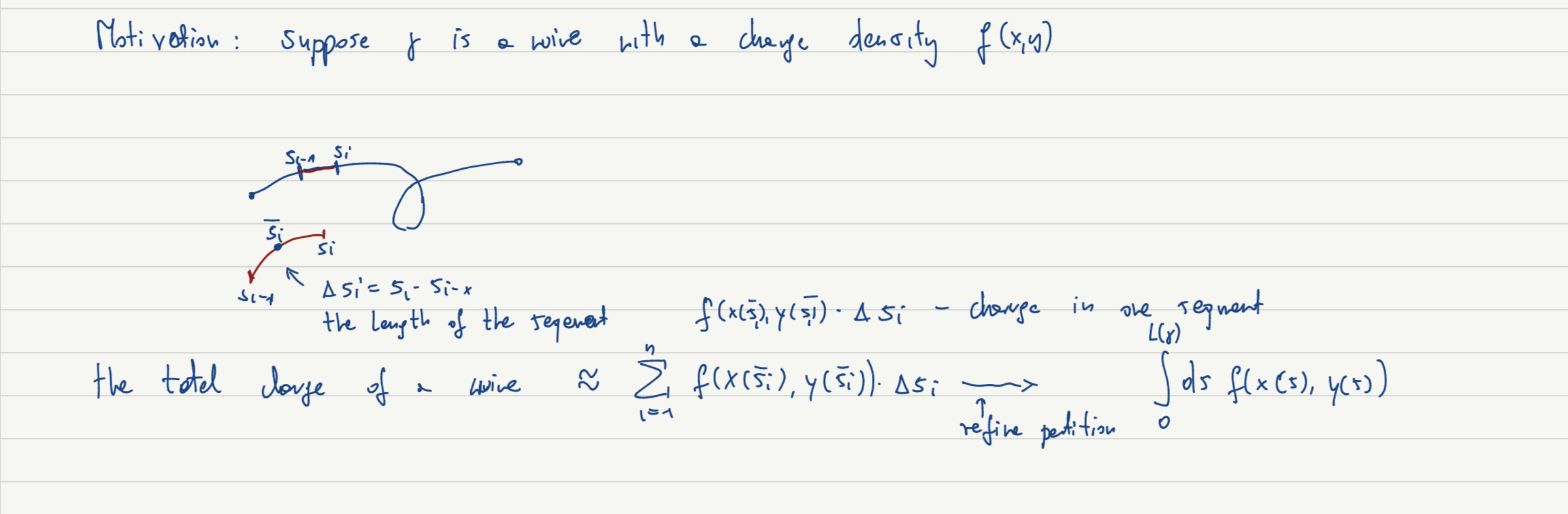
Then we get the final result

The reasons why we need this way of parametrization is that sometimes we cannot using the first
methd, the direct parametrization to solve the problems. For instance the arc length of the
ellipse. The essence of the arc length parametrization is that its Riemann sum to get the
length changed to every small piece of distance which is the true arc length rather than the
approximation of the arc length using the first derivative.

Here is the example